In all things holy, we look for beauty.
“Tyger! Tyger! burning bright
In the forest of the night,
What immortal hand or eye
Could frame thy dreadful symmetry?”
William Blake.
 “The mind of God appears to be abstract but not complicated. He also appears to like group theory.”
Anthony Zee in “Fearful Symmetry”.
“The mind of God appears to be abstract but not complicated. He also appears to like group theory.”
Anthony Zee in “Fearful Symmetry”.
“You know what Aquinas says: The three things requisite for beauty are, integrity, a wholeness, symmetry and radiance.” James Joyce in “Stephen Hero”
INTRODUCTION.
 |
| Flower Rosette for Bowed Psaltery (Inspired Instruments) |
“Fundamental physicists are sustained by the faith that ultimate design is suffused with symmetries.”
It is also true that beauty/elegance do not in themselves suffice to establish truth in science; there has to be empirical verification for a theory in order for it be scientifically valid and useful, so we will show below how some beautiful theories were negated by experiment. In our story the Higgs boson will not be the main character; rather it will (to switch analogies) be a coda to a symphony (as in Beethoven’s 8th).
SYMMETRY AND PHYSICS–INTRODUCTION
 |
| Celtic Knot Rosette for Bowed Psaltery (Inspired Instruments) |
A BRIEF HISTORY OF THE STANDARD MODEL: SYMMETRY = THEORY
In this short piece I can’t hope to give an adequate summary of the development of modern physics, the discovery of fundamental particles (or, as thought in the 1930′s and 40′s, what were thought to be fundamental), the electron, neutron, proton, positron, neutrino, photon. For the reader who wants to read about this history and the development of the Standard Model in more detail, there are several good references: “Fearful Symmetry” by A. Zee, “Not Even Wrong” by Peter Voit, “The Hunting of the Quark” by Peter Riordan, or “Deep Down Things” by Bruce Schumm. There are articles in Wikipedia on particle physics and the Standard Model.
 |
| Triune Celtic Knot Rosette for Bowed Psaltery (Inspired Instruments) |
“You, Lord, created heaven and earth.
They are beautiful because You are beauty.
They are good because You are goodness.
They exist because You are existence.”
Confessions, 11,4
SOME FUNDAMENTAL IDEAS.Before laying out a very brief account of the standard model and the Higgs field/boson, I want to give a qualitative explanation of some basic physical and mathematical concepts. A fine account, which has a somewhat different emphasis than I will take, is given by a Dutch physicist, Marcel van Velzen
FIELD/FORCE PARTICLE EQUIVALENCE.
Fields are essentially forces, varying in strength and direction through space. The notion of a field was introduced back in the early part of the 19th century by Michael Faraday studying magnetic forces. (See picture of the magnetic field–array of iron filings over a bar magnet).
Fields are essentially forces, varying in strength and direction through space. The notion of a field was introduced back in the early part of the 19th century by Michael Faraday studying magnetic forces. (See picture of the magnetic field–array of iron filings over a bar magnet).
 |
| Magnetic Field: Iron Filings over Bar Magnet |
The electromagnetic field consists of electric and magnetic fields alternating in strength and direction like waves, propagating through space. Light is in fact an electromagnetic field. Now light can also (as Einstein first showed) behave as particles, photons. This is an aspect of the “wave-particle” duality that lies at the heart of quantum mechanics. Since charged particles (electrons, protons) interact via the electromagnetic field, they can also be thought to interact via the exchange of “virtual photons”, as illustrated below.
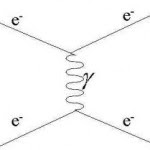 |
| electon(e-) / electron(e-) interaction via virtual photon (gamma) |
SOME IDEAS ABOUT SYMMETRY.
Symmetry has to do with sameness when things are rearranged or moved. A good illustration of symmetry is shown by the inset figures of bowed psaltery rosettes: if appropriate rotations (about axes perpendicular to the plane or in the plane) or mirror reflections are done, the rosettes will look the same. Now there is another kind of symmetry important for particle physics, permutation symmetry. Let’s consider identical triplets with labels 1,2,3 (see figure). (The triplets aren’t quite identical, but let that pass.)
Suppose the babies are switched around in position and the labels removed–neglecting such distinguishing features as positions of legs, etc,(and parents’ special knowledge of distinguishing features); then the total picture will look the same. So the idea of permutation symmetry is that if we disregard arbitrary labels on otherwise indistinguishable objects, they can be switched around in position and there will be no way to tell the difference between the original and the modified arrangement.
Symmetry has to do with sameness when things are rearranged or moved. A good illustration of symmetry is shown by the inset figures of bowed psaltery rosettes: if appropriate rotations (about axes perpendicular to the plane or in the plane) or mirror reflections are done, the rosettes will look the same. Now there is another kind of symmetry important for particle physics, permutation symmetry. Let’s consider identical triplets with labels 1,2,3 (see figure). (The triplets aren’t quite identical, but let that pass.)
 |
| Triplets (almost identical) |
Mathematical tools for dealing with symmetry are given by group theory; I’ll try to list a few of the important ideas here and give a more detailed example below. A mathematical group is a collection of elements which obey particular multiplication rules (rules of successive operations). The group is such that any multiplication gives one and only one member of the group, the group contains the identity element I (that is, multiplication by I is like multiplying by 1–it doesn’t change anything), and to each element there is a corresponding inverse (multiplying successively by an element and its inverse gives the identity I). Here’s an abstract, but simple example: the elements I,A such that IxA = AxI =I and AxA=I (i.e. A is its own inverse). The group would be realized (the math term for a concrete example) in the permutations of two identical objects labeled with the numbers 1 and 2, and put in an order (1,2): the identity I would be (1,2)–>(1,2), leaving the objects alone; the element A would be (1,2)–>(2,1), interchanging the order of the objects. If we interchanged twice, AxA, we would get back to the original order, i.e. the identity operation, I. This group would also be realized by symmetry operations on objects such as the capital letter Z (rotation by 180 degrees about an axis perpendicular to the plane).
One very important feature of group theory for the Standard Model is the notion of representations. A representation is a collection of matrices which obey the same multiplication rules as the group. The size of the matrix (how many rows or columns) will correspond to the number of objects it acts on; for example, a 3×3 matrix will act on three objects.
SYMMETRY AND PARTICLE PERIODIC TABLES.
I hope at least some of you remember from high school Chemistry how Mendelyev’s Periodic Table helped make sense of the order of elements and their chemical behavior. In a similar way one can arrange fundamental particles into symmetric tables, arrangements which turn out to be explained by group theory, in the same way that the chemical periodic table was explained by quantum mechanics. Below is an example of such a table:
SYMMETRY AND PARTICLE PERIODIC TABLES.
I hope at least some of you remember from high school Chemistry how Mendelyev’s Periodic Table helped make sense of the order of elements and their chemical behavior. In a similar way one can arrange fundamental particles into symmetric tables, arrangements which turn out to be explained by group theory, in the same way that the chemical periodic table was explained by quantum mechanics. Below is an example of such a table:
 |
| Quart Octer from Cronodon.com (http://cronodon.com/Atomic/QCD.html) |
What does all this have to do with group theory? Group theory tells us that for a given symmetry, the dimensions of the various possible representations are fixed. So, for example, for SU(3) symmetry there will be a representation of dimension 8 (as in the diagram above) which will have two doublet states (the n and p and the Chi – and Chi 0 rows) a triplet state (the Sigma -, 0, and + row) and a singlet state (the lambda 0 row). There would not be representations of dimensions 7 or 9, for SU(3) symmetry, so that if a septet or nonet state were observed, that would belie an SU(3) symmetry. For SU(3) symmetry there is also a representation of dimension 10, which is realized below in the decuplet of very short-lived baryons (observed as “resonances” in particle physics) with total spin 3/2.
 |
| Baryon Decuplet (10-fold) |
GAUGE INVARIANCE SYMMETRY.
A critical and foundational element in contemporary physical theory is gauge invariance. Gauge invariance is a type of local symmetry, that is to say, symmetry is given at various points, but changes as you move. The symmetry is not global, i.e. is not the same throughout the space (refer to the image below, taken from the Wikipedia article linked above):
Local twisting of up and down coordinates (Cartesian coordinates) to illustrate gauge invariance (taken from linked Wikipedia article). Note that gauge invariant theories (e.g. general relativity, quantum field theory) would be valid at each point, despite the twisting and stretching of the coordinate system.
Imposing gauge symmetry will greatly restrict the physics and yield carrier particle(s) for the fields: for quantum electrodynamics (QED) theory, the photon results. More general gauge invariant theories (e.g. Yang-Mills theory, see below), yield gauge bosons to carry the fields. The term “gauge” came from Hermann Weyl in his 1915 work on gauge invariance in electromagnetic theory and relativity–he used the term to relate to “distance” and its changes (as, for example, the distance between railroad tracks).
SYMMETRY BREAKING
An important notion in theoretical physics is that of symmetry breaking (follow the link in the heading above for a detailed explanation). Here is a relatively simple example: consider a drop of water (say, as a particle in mist), roughly spherical in shape and therefore highly symmetric; let the temperature fall to the freezing point and the drop will spontaneously turn into a snowflake (or an ice crystal) of lower symmetry. Another example is that of an iron bar that at sufficiently low temperature becomes magnetized (all small magnetic domains in the bar line up in the same direction), giving a direction (that of the magnet N to S poles) and thereby lowering the symmetry (which prior to the magnetization did not have a specified direction). Symmetry breaking plays a fundamental role in the Higgs field; it is the mechanism by which the Higgs field endows fundamental particles with mass. Symmetry breaking is depicted in the “Mexican Hat” potential shown below (a similar diagram was shown in Higgs’ original article proposing this potential and mechanism for symmetry breaking).
SYMMETRY BREAKING
An important notion in theoretical physics is that of symmetry breaking (follow the link in the heading above for a detailed explanation). Here is a relatively simple example: consider a drop of water (say, as a particle in mist), roughly spherical in shape and therefore highly symmetric; let the temperature fall to the freezing point and the drop will spontaneously turn into a snowflake (or an ice crystal) of lower symmetry. Another example is that of an iron bar that at sufficiently low temperature becomes magnetized (all small magnetic domains in the bar line up in the same direction), giving a direction (that of the magnet N to S poles) and thereby lowering the symmetry (which prior to the magnetization did not have a specified direction). Symmetry breaking plays a fundamental role in the Higgs field; it is the mechanism by which the Higgs field endows fundamental particles with mass. Symmetry breaking is depicted in the “Mexican Hat” potential shown below (a similar diagram was shown in Higgs’ original article proposing this potential and mechanism for symmetry breaking).
 |
| Mexican Hat Potential |
If you look at the Mexican Hat potential (so-called because it looks like a sombrero) and the wine bottle with the punt (the hill at the bottom) you’ll see that they have a circular symmetry. Now consider what would happen if you put a small ball (very gently) into the center of a bottle without a punt, just a flat bottom. It would stay in the bottom at the center and there would still be circular symmetry. Now consider what would happen if you put the ball into the bottle with the punt, setting it at the top of the punt–it might stay, but that would be an unstable equilibrium, and the ball would most likely roll to the side of the bottle. The circular symmetry would thereby be broken, because the position of the ball at the side of the bottle defines a unique direction. The same thing will happen with the Mexican Hat (Higgs) potential. A system at the top of the central hill will spontaneously descend to the lower energy at the rim, and thereby break the circular symmetry.
YANG-MILLS THEORY
The cornerstone of the Standard Model is Yang-Mills theory. The theory was proposed in 1954 by Chen Yang and Robert Mills as a generalization of gauge-invariant quantum electrodynamics, which had been remarkably successful. The goal was to give a theory for the strong nuclear interaction. However, the theory was not successful: it predicted the existence of massless carrier bosons (in addition to a photon), which were not observed.
THE HIGGS FIELD/BOSON
The Higgs field was proposed by Peter Higgs in 1965 as a way to bring spontaneous symmetry breaking into Yang-Mills theory. The Higgs field generates mass for particles in the following way, as nicely explained by Van Velzen (see link above). Consider the fundamental property of mass, inertia: according to Newton’s Laws of Motion: a particle moving with constant velocity in a straight line will continue to move in a straight line unless acted on by a force; if acted on by a force its velocity will change (acceleration will occur according to the famous equation F=ma). Mass enters by requiring a force to change velocity (accelerate the particle), the force being proportional to mass for given acceleration. If a particle does not have mass, it’s velocity will be constant, as is that of the massless photon, which has the speed c, the speed of light. One can think of the Higgs field acting as a repulsive lattice; that is, one can imagine a regular array of points, which are sources of equal repulsive forces. Lattice points behind a particle will push the mass particle forward; lattice points in front of the mass particle will push it backward with equal force; the effect will then, as the diagram given by Van Velzen shows so well, be for the particle to move with constant velocity. (Note: the explanation given by many popular accounts of the Higgs field, as if a particle were moving in a viscous fluid, is not correct; if that were so then the particle would decelerate and stop moving).
ELECTROMAGNETISM+WEAK INTERACTION=”ELECTROWEAK” THEORY. Sheldon Glashow extended the Yang-Mills theory to cover both electromagnetism and the weak interaction (beta-decay) in 1960. However, his theory was deficient in that it was not gauge-invariant; the masses of the carrier bosons were specified explicitly. In 1967 Steven Weinberg and Abdus Salam independently proposed a truly gauge-invariant version of Glashow’s theory; they achieved this by adding the Higgs field to the theory, thereby yielding spontaneous symmetry breaking with massive carrier bosons. The theory was confirmed experimentally in 1973 by finding “neutral currents” in neutrino scattering and in 1983 by the detection of the carrier bosons, W and Z.
QUANTUM CHROMODYNAMICS = “QCD”
The next extension of Yang-Mills theory in the Standard Model was quantum chromodynamics, QCD, the theory to explain the strong interaction between quarks, the particle constituents of protons, neutrons and other heavy particles (baryons). Glashow, Salam and Weinberg were jointly awarded the Nobel prize in 1979 for this theory.Experimental evidence strongly suggested the existence of three types of quarks, i.e. three types for each of the six different quark “flavors”–up, down, strange, top, bottom, charm; the three types differ in a degree of freedom that is called color, but were otherwise identical in mass, charge, etc, (the quark color has no relation to colors observed in the ordinary world). Thus there are “red”, “blue”, “green” up quarks, “red”, “blue”, “green” down quarks, etc., as shown in the illustration (from the Wikipedia article on Quarks linked above).
The quarks are bound within a baryon (nuclear or other heavy particle) by carrier bosons termed “gluons”. A strange, but theoretically justified and experimentally verified property of the force binding the quarks inside a baryon, is that the force becomes vanishingly small as the quarks get close to each other but becomes increasingly strong as they get distant, so that effectively the quarks are bound within a particle and can’t get out. This latter behavior is called “quark confinement” and while models for it have been proposed (e.g. like the elastic force of a very strong rubber band), the exact mathematical justification is yet to be achieved.
GRAND UNIFICATION THEORY = “GUT”
An obvious next step in the standard model is to give a theory in which electromagnetism, the weak interaction, the strong force and gravity are all derived from a common gauge theory, analogous to the derivation of electromagnetism and the weak interaction from the electroweak theory. There were a number of attempts following the success of QCD to find a theory that would unify all various types of forces and interactions. The first of these was given by Sheldon Glashow and Howard Georgi in 1974, who proposed a gauge invariant theory combining symmetries for electromagnetism, the weak, and the strong interactions. Unfortunately the theory failed a crucial experimental test: it predicted a much shorter decay rate for protons (by a factor of 100 to 10,000) than the lower limit determined experimentally. Other proposed theories also fell short, and the attention of theoretical physicists turned to other “theories of everything” (TOE’s)–supersymmetry, string theory, M-theory–which I won’t discuss.
YANG-MILLS THEORY
The cornerstone of the Standard Model is Yang-Mills theory. The theory was proposed in 1954 by Chen Yang and Robert Mills as a generalization of gauge-invariant quantum electrodynamics, which had been remarkably successful. The goal was to give a theory for the strong nuclear interaction. However, the theory was not successful: it predicted the existence of massless carrier bosons (in addition to a photon), which were not observed.
THE HIGGS FIELD/BOSON
The Higgs field was proposed by Peter Higgs in 1965 as a way to bring spontaneous symmetry breaking into Yang-Mills theory. The Higgs field generates mass for particles in the following way, as nicely explained by Van Velzen (see link above). Consider the fundamental property of mass, inertia: according to Newton’s Laws of Motion: a particle moving with constant velocity in a straight line will continue to move in a straight line unless acted on by a force; if acted on by a force its velocity will change (acceleration will occur according to the famous equation F=ma). Mass enters by requiring a force to change velocity (accelerate the particle), the force being proportional to mass for given acceleration. If a particle does not have mass, it’s velocity will be constant, as is that of the massless photon, which has the speed c, the speed of light. One can think of the Higgs field acting as a repulsive lattice; that is, one can imagine a regular array of points, which are sources of equal repulsive forces. Lattice points behind a particle will push the mass particle forward; lattice points in front of the mass particle will push it backward with equal force; the effect will then, as the diagram given by Van Velzen shows so well, be for the particle to move with constant velocity. (Note: the explanation given by many popular accounts of the Higgs field, as if a particle were moving in a viscous fluid, is not correct; if that were so then the particle would decelerate and stop moving).
ELECTROMAGNETISM+WEAK INTERACTION=”ELECTROWEAK” THEORY. Sheldon Glashow extended the Yang-Mills theory to cover both electromagnetism and the weak interaction (beta-decay) in 1960. However, his theory was deficient in that it was not gauge-invariant; the masses of the carrier bosons were specified explicitly. In 1967 Steven Weinberg and Abdus Salam independently proposed a truly gauge-invariant version of Glashow’s theory; they achieved this by adding the Higgs field to the theory, thereby yielding spontaneous symmetry breaking with massive carrier bosons. The theory was confirmed experimentally in 1973 by finding “neutral currents” in neutrino scattering and in 1983 by the detection of the carrier bosons, W and Z.
QUANTUM CHROMODYNAMICS = “QCD”
The next extension of Yang-Mills theory in the Standard Model was quantum chromodynamics, QCD, the theory to explain the strong interaction between quarks, the particle constituents of protons, neutrons and other heavy particles (baryons). Glashow, Salam and Weinberg were jointly awarded the Nobel prize in 1979 for this theory.Experimental evidence strongly suggested the existence of three types of quarks, i.e. three types for each of the six different quark “flavors”–up, down, strange, top, bottom, charm; the three types differ in a degree of freedom that is called color, but were otherwise identical in mass, charge, etc, (the quark color has no relation to colors observed in the ordinary world). Thus there are “red”, “blue”, “green” up quarks, “red”, “blue”, “green” down quarks, etc., as shown in the illustration (from the Wikipedia article on Quarks linked above).
 |
| Colors of Up (u) and Down (d) quarks in a proton |
GRAND UNIFICATION THEORY = “GUT”
An obvious next step in the standard model is to give a theory in which electromagnetism, the weak interaction, the strong force and gravity are all derived from a common gauge theory, analogous to the derivation of electromagnetism and the weak interaction from the electroweak theory. There were a number of attempts following the success of QCD to find a theory that would unify all various types of forces and interactions. The first of these was given by Sheldon Glashow and Howard Georgi in 1974, who proposed a gauge invariant theory combining symmetries for electromagnetism, the weak, and the strong interactions. Unfortunately the theory failed a crucial experimental test: it predicted a much shorter decay rate for protons (by a factor of 100 to 10,000) than the lower limit determined experimentally. Other proposed theories also fell short, and the attention of theoretical physicists turned to other “theories of everything” (TOE’s)–supersymmetry, string theory, M-theory–which I won’t discuss.
SUMMATION.
The Standard Model, while being a beautiful and coherent physical theory, does, nevertheless have deficiencies and problems. I won’t talk about these in detail here; Woit’s book, “Not Even Wrong” and the grand text by Roger Penrose, “The Road to Reality”, discuss these problems in more detail. You can also do a web search “Problems with the Standard Model” and find lots of sites; the problems listed in these sites overlap but do not all coincide. In general, one can say that these problems are of a sort, “why?”–e.g. wherefore six flavors of quarks, or three generations of baryons; why does the negative of the electron equal in magnitude the positive charge of the proton (fortunately, for the existence of the universe); whence comes the violation of parity? Nevertheless, the Standard model is an impressive structure. To use an architectural analogy, the Standard model is an arch, the keystone of which is the Higgs field, and it rests on a foundation of basic theory. Many scientists have contributed to the structure: to the foundation, Maupertuis, Noether, Weyl, with principles of least action, symmetry and conservation, and gauge invariance; to the arch itself, Glashow, Weinburg, Salam, and the many other theoretical physicists–Yang, Mills, Anderson, Wilson,t’Hooft, Veltman, Gross, Politzer, Wilczek–who contributed essential pieces to the theory.
 And what does all this have to do with the title of this piece, God, Symmetry and Beauty? I’m going to leave that to a new piece. This has been a labor (in the child-bearing sense) much drawn-out and with great pain. As a colleague told me, the best way to learn about a subject is to teach it, and I have gone back to graduate quantum mechanics courses to review stuff I’d forgotten (not used in my research), gone to papers (Higgs original letter) to understand material that I had never needed or used, and thus have learned much. I’m not sure whether more than the flavor (like those little spoonfuls at the ice cream store) has been conveyed, but those readers who do want to explore this topic in more depth should go to the books by Zee and Woit, and those links given in this paper.
And what does all this have to do with the title of this piece, God, Symmetry and Beauty? I’m going to leave that to a new piece. This has been a labor (in the child-bearing sense) much drawn-out and with great pain. As a colleague told me, the best way to learn about a subject is to teach it, and I have gone back to graduate quantum mechanics courses to review stuff I’d forgotten (not used in my research), gone to papers (Higgs original letter) to understand material that I had never needed or used, and thus have learned much. I’m not sure whether more than the flavor (like those little spoonfuls at the ice cream store) has been conveyed, but those readers who do want to explore this topic in more depth should go to the books by Zee and Woit, and those links given in this paper.
 |
| Arch with Keystron--The Arch symbolizes the Standard Model and the Keystone Symbolizes the Higgs Field/Boson |
 And what does all this have to do with the title of this piece, God, Symmetry and Beauty? I’m going to leave that to a new piece. This has been a labor (in the child-bearing sense) much drawn-out and with great pain. As a colleague told me, the best way to learn about a subject is to teach it, and I have gone back to graduate quantum mechanics courses to review stuff I’d forgotten (not used in my research), gone to papers (Higgs original letter) to understand material that I had never needed or used, and thus have learned much. I’m not sure whether more than the flavor (like those little spoonfuls at the ice cream store) has been conveyed, but those readers who do want to explore this topic in more depth should go to the books by Zee and Woit, and those links given in this paper.
And what does all this have to do with the title of this piece, God, Symmetry and Beauty? I’m going to leave that to a new piece. This has been a labor (in the child-bearing sense) much drawn-out and with great pain. As a colleague told me, the best way to learn about a subject is to teach it, and I have gone back to graduate quantum mechanics courses to review stuff I’d forgotten (not used in my research), gone to papers (Higgs original letter) to understand material that I had never needed or used, and thus have learned much. I’m not sure whether more than the flavor (like those little spoonfuls at the ice cream store) has been conveyed, but those readers who do want to explore this topic in more depth should go to the books by Zee and Woit, and those links given in this paper.

No comments:
Post a Comment